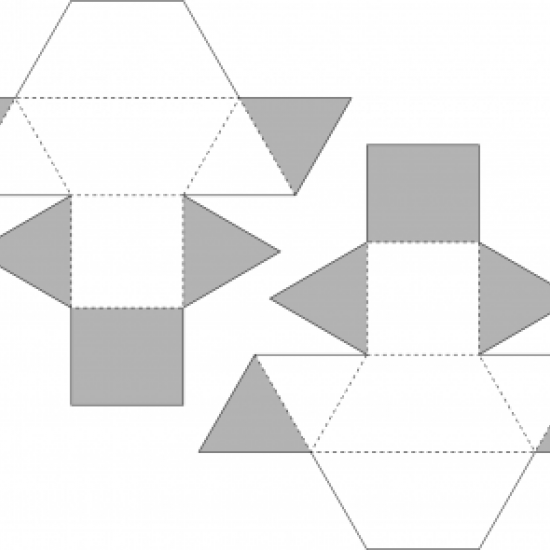
Un puzzle en 3D formant un cube, composé de 24 tétraèdres, tous de même volume. Huit sont des tétraèdres réguliers, seize sont des "quarts d’octaèdre", dont le patron est composé de deux triangles équilatéraux et deux moitiés de carré (la diagonale, de longueur $\sqrt 2$ par rapport à toutes les autres arêtes, est le côté du cube).
Le but du kit est de comprendre que tous les tétraèdres ont même volume, d’en déduire en particulier qu’un octaèdre régulier a le même volume que quatre tétraèdres réguliers et d’en finir avec le volume d’un tétraèdre de côté a :
$$ V(\mathcal T_\alpha) = \frac {(a\sqrt 2)^3}{24}.$$
Vous pouvez composer ces 24 tétraèdres à partir de leurs patrons. Cependant le volume devrait être proportionnel à la masse, il serait donc meilleur d’avoir des versions pleines. À Lyon, nous avons un kit fabriqué par Pierre Gallais, en résine, de trois couleurs différentes. C’est une évolution des puzzles "le doublement du tétraèdre" et "le doublement de la pyramide" qui font partie de Math@Lyon, extrait de l’exposition "Pourquoi les mathématiques ?".
Pas de kit disponible pour cette activité





Quelques liens supplémentaires :